Габаритные размеры рав 4: Технические характеристики авто Toyota RAV4
габаритные размеры, технические характеристики, мощность двигателя, максимальная скорость, специфические особенности эксплуатации и ухода, отзывы владельцев
Кроссоверы в последние годы занимают первые строчки по продажам во всем мире. Toyota RAV 4 не стала исключением, модель успешно раскупается и эксплуатируется во всех уголках земного шара. Габаритные размеры «Тойота РАВ 4» становятся все больше от поколения к поколению. Но это не помешало автомобилю оставаться в классе компактных кроссоверов и радовать свою аудиторию новыми опциями и кузовами.
История
В 1989 году японские инженеры начали работу над автомобилем, который должен был сочетать в себе небольшой универсал с полным приводом и обеспечил бы свободное передвижение не только по городу, но и выезд на природу. Идея развилась только к 1995 году, тогда и было представлено первое поколение «РАВ 4». Автомобиль выпускался в пятидверном и трехдверном кузовах, оснащался полным приводом с автоматической или механической трансмиссией на выбор, под капотом устанавливался двухлитровый бензиновый двигатель.
Тойота РАВ 4 с вариатором : последние отзывы, технические…
«Тойота РАВ 4» — это эргономичный и стильный кроссовер городского типа, который не только…
Выпуск второго поколения состоялся в 2006 году. Автомобиль полностью переработали, он получил обновленный дизайн кузова, новый салон и более мягкую подвеску. Габаритные размеры «Тойота РАВ 4» существенно изменились в большую сторону. Кроссовер получил доработанный силовой агрегат, а новое шасси подарило автолюбителям превосходную управляемость и уверенность на любом дорожном покрытии. Кузов по-прежнему был доступен в пятидверном и трехдверном исполнении.
В 2009 году появилось следующее поколение RAV 4. Существенно изменились габариты «Тойота РАВ 4». 3 поколение получило полностью обновленный внешний вид, небольшие изменения в технических характеристиках. Безопасность пассажиров перешла на новый уровень – в базовой комплектации уже доступно 7 подушек SRS. Увеличенный дорожный просвет повысил уверенность на грунтовых дорогах.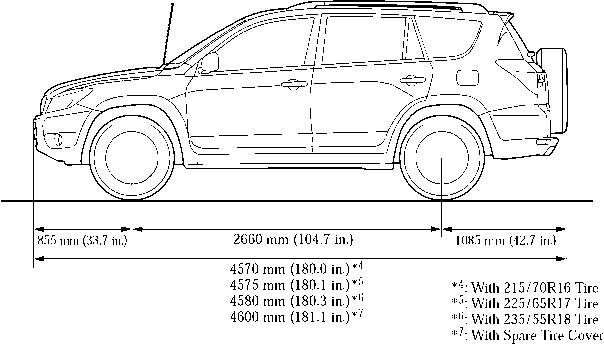 Кузов теперь выпускался только в пятидверном исполнении.
Кузов теперь выпускался только в пятидверном исполнении.
Тойота Рав 4 4 поколения: фото, отзывы владельцев,…
Автомобиль «Тойота Рав 4» берет свое начало в далеком 1994-м году. Именно тогда на свет появилось…
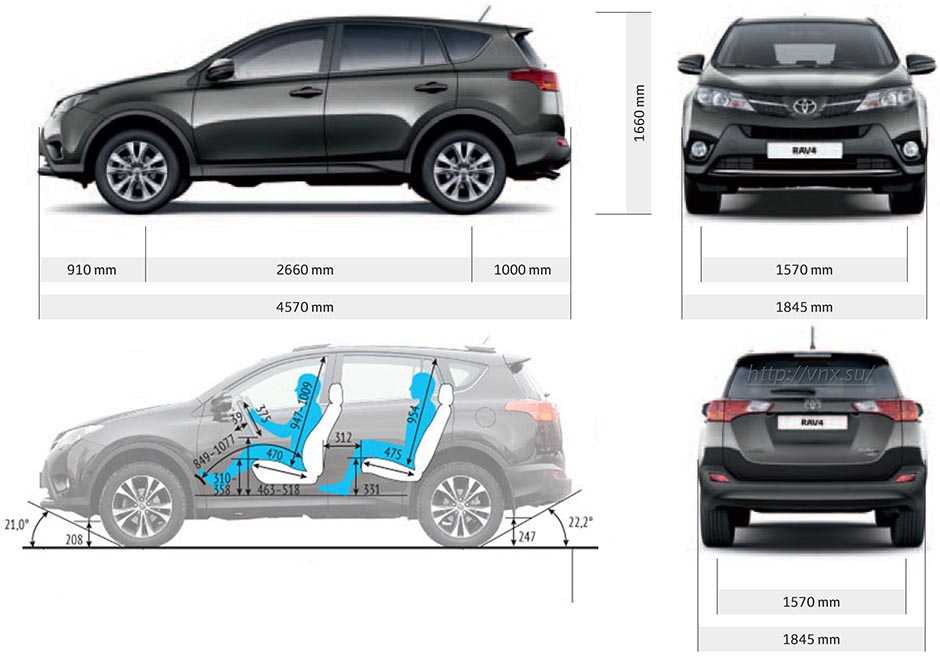
Размеры авто «Тойота РАВ 4» увеличивались от поколения к поколению. Четвертая генерация не стала исключением. Японские инженеры воссоздали кузов полностью с нуля, агрессивный современный дизайн автомобилей 2013 года не сразу понравился автолюбителям. Однако спустя некоторое время кроссовер снова начали активно покупать. Улучшенная система полного привода, трансмиссия, двигатель и шасси сделали свое дело – автомобиль обрел былую популярность.
Отзывы владельцев
Автовладельцы ставят высокие оценки кроссоверу любого поколения. Отличная проходимость, точное и предсказуемое рулевое управление, высокий клиренс – главные достоинства автомобиля. Габаритные размеры «Тойота РАВ 4» также устраивают пользователей: с багажником и местом для задних пассажиров все в полном порядке. Соотношение цены и качества всегда позволяет занимать всем автомобилям марки Toyota первые места в списках продаж.
Соотношение цены и качества всегда позволяет занимать всем автомобилям марки Toyota первые места в списках продаж.
Из минусов следует отметить стираемость колодок тормозной системы, порой замена элементов требуется каждые 15 000–20 000 пробега. Также некоторые владельцы жалуются на неравномерный прогрев салона в холодное время года.
Новый Прадо (2018): последние отзывы и комплектация
Комфортабельный внедорожник с полным приводом «Прадо» образца 2018 года с возможностью…
По работе трансмиссии и двигателя, при своевременном прохождении ТО никаких нареканий не возникает. Поэтому никаких особенностей по уходу при эксплуатации автомобиля нет.
Новый RAV 4. Экстерьер
Чаще всего при смене поколения автопроизводители с особой осторожностью относятся к изменению дизайна автомобиля. Но японские инженеры решились на кардинальные перемены в имидже обновленного кроссовера. Дизайнеры однозначно сделали ставку на брутальность, полностью разработав дизайн с нуля.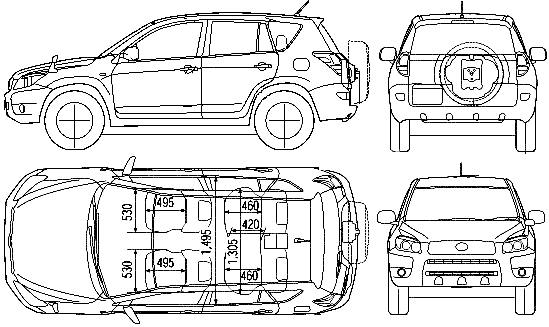
Фронтальная часть получила новый бампер с ярко выраженной защитной накладкой из черного пластика. Противотуманные фары посажены высоко от дороги и утоплены внутрь для защиты от повреждений. Линия капота стала немного выше и плавно переходит в остроугольную оптику со встроенными светодиодными огнями. Трапециевидная решетка радиатора состоит из крупных сот, в которые встроены датчики парковки.
Корма обзавелась современными фонарями с резкой рубленой формой, яркими светодиодами и хромированным молдингом. Укороченный бампер также надежно прикрыт защитным пластиком, снизу расположились две выхлопные трубы. На крыше – акулий плавник и резкий скос в угоду аэродинамике. Крышка багажника по-прежнему сохранила прямоугольную форму и обеспечивает комфортный доступ в багажное отделение.
Сбоку автомобиль выглядит агрессивно и современно. Лобовое стекло с сильным уклоном переходит в плавную крышу, оборудованную рейлингами. Кстати, цвет крыши теперь может отличаться от основного цвета кузова.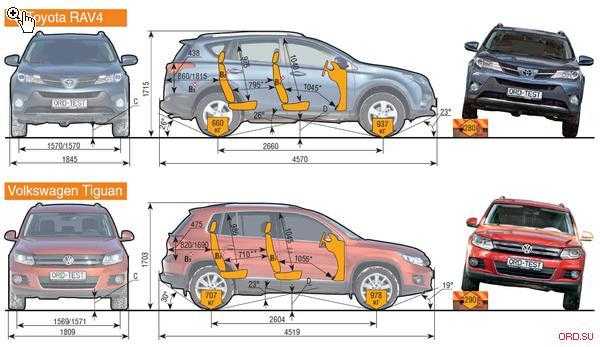 Линия окон с ярко выраженным уклоном и крупными зеркалами с повторителями поворотов, колесные арки с пластиковыми накладками квадратной формы и огромные алюминиевые диски 19 диаметра отлично дополняют образ передней и задней части кроссовера. Все детали выполнены в одном стиле, и ничего не выглядит чужеродно.
Линия окон с ярко выраженным уклоном и крупными зеркалами с повторителями поворотов, колесные арки с пластиковыми накладками квадратной формы и огромные алюминиевые диски 19 диаметра отлично дополняют образ передней и задней части кроссовера. Все детали выполнены в одном стиле, и ничего не выглядит чужеродно.
Кузов получил новые размеры:
- длина 4595 миллиметров;
- ширина 1854 миллиметра;
- высота 1699 миллиметров;
- ширина колесной базы 2690 миллиметров;
- дорожный просвет 210 мм.
Интерьер
В кроссовере разместится водитель любого роста и комплекции. Удобный руль спортивной формы обшит кожаной оплеткой и оборудован внушительным количеством клавиш. Приборная панель выполнена в классическом стиле со стрелками вместо электронных шкал, а в середине шкалы спидометра разместился крупный дисплей бортового компьютера. Читаемость приборов на высоте в ночное и солнечное время. Центральная консоль собрана из качественного пластика, широкий центральный подлокотник обшит кожей. Климат-контроль с большим количеством кнопок плавно переходит в ручку КПП с опрятной хромированной окантовкой, а над всем этим возвышается яркий и четкий 7- или 8-дюймовый дисплей (зависит от комплектации).
Климат-контроль с большим количеством кнопок плавно переходит в ручку КПП с опрятной хромированной окантовкой, а над всем этим возвышается яркий и четкий 7- или 8-дюймовый дисплей (зависит от комплектации).
«Тойота РАВ 4», размер салона которого раздался в ширину и в длину, получила новые кресла с анатомическим профилем и ярко выраженной боковой поддержкой, подогревом и вентиляцией. Панорамный люк, акустическая система JBL с 11 динамиками, беспроводная зарядка для мобильных устройств, цифровое зеркало заднего вида и многие другие опции способны удивить даже самого избалованного водителя. Улучшенная шумоизоляция, качественная система мультимедиа и выверенная точность климат-контроля с комфортом позволяют преодолевать большие расстояния без намека на усталость. Единственным раздражающим фактором может стать яркая синяя подсветка приборов и кнопок, которая многим не нравится и утомляет глаза.
Багажное отделение
Доступ в багажное отделение стал еще удобнее. Достаточно легкого взмаха ноги под бампером кроссовера, и большая прямоугольная дверь, оснащенная электроприводом, начинает быстрое уверенное движение. «Тойота РАВ 4», размеры багажника которой в настоящее время тщательно скрываются, имеет два дополнительных места в грузовом отделении и складывающиеся спинки задний сидений для увеличения грузового пространства. Также заявлено появление мощного сабвуфера и дополнительного прикуривателя.
«Тойота РАВ 4», размеры багажника которой в настоящее время тщательно скрываются, имеет два дополнительных места в грузовом отделении и складывающиеся спинки задний сидений для увеличения грузового пространства. Также заявлено появление мощного сабвуфера и дополнительного прикуривателя.
Силовая установка
Силовая установка «РАВ 4» для российского рынка получит 2- и 2,5-литровый бензиновый двигатель (149 и 180 л. с.) и дизель объемом 2,2 литра (150 л. с.). Все установки проверены годами и не требуют особенных условий обслуживания. Расход в смешанном цикле не превышает 9 литров на сотню, разгон занимает около 9,3 секунд на 2,5-литровом моторе, на «двушке» — 10,3 с. Максимальная скорость ограничена показателем в 180 км/ч. Коробка передач заявлена автоматическая с 8 ступенями для США и вариаторная (CVT) для остальных рынков, в том числе и для России.
Самым главным нововведением стала система полного привода, способная передать до 50 процентов крутящего момента на заднюю ось при определенных условиях, что позволило существенно повысить проходимость кроссовера.
Шасси не коснулись какие-либо серьезные изменения, несмотря на смену платформы – многорычажная схема сзади и «МакФерсон» спереди. Все достаточно просто и надежно.
Выводы
Габаритные размеры «Тойота РАВ 4» позволят разместить пассажиров с большим комфортом и не повлияют на остроту управляемости за счет улучшенных аэродинамических характеристик. Полностью новый облик автомобиля больше направлен на мужскую аудиторию и обладает резкими и четкими гранями, плавные полукруглые формы остались в прошлом. Инженеры «Тойота» всеми силами хотели изменить дизайн «РАВ 4» в более дерзкую и современную сторону, при этом не растеряв практичности, надежности и проходимости автомобиля. И у них это получилось.
Тойота РАВ4 2001 габаритные размеры: клиренс, длина, высота
Габаритные размеры Тойота РАВ4 2001
Автолюбители частенько ищут данные про такие популярные автомобильные габариты как длина, ширина и высота авто, когда сомневаются, заедет ли их железный конь в гараж либо же не хотят иметь проблем с парковкой в городе. Вопрос габаритов авто также зачастую волнует начинающих водителей либо же людей, которые задумали сменить машину.
Вопрос габаритов авто также зачастую волнует начинающих водителей либо же людей, которые задумали сменить машину.
Стоит понимать, что помимо базовых габаритов есть еще и другие параметры, на которые стоит обратить внимание. Например, более короткая колесная база повышает маневренность, что немаловажно, если вам приходится много лавировать в городском потоке по узким улочкам, вписываться в крутые повороты и т.д. С другой стороны, удлиненная колесная база придает автомобилю устойчивости, правда, она же заставляет быть предельно осторожным при переезде высоких преград, бугров и кочек.
Внешние размеры Тойота РАВ4 2001
| Длина машины | 424.434 см |
| Ширина | 173.482 см |
| Высота | 166.878 — 167.894 см |
| Колесная база | 248. 92 см 92 см
|
| Радиус разворота | 44.958 см |
| Клиренс | |
| Коэффициент аэродинамического сопротивления | 0.4 |
| Передняя колея | 150.622 см |
| Задняя | 149.606 — 150.114 см |
Передняя и задняя ширина колеи автомобиля Тойота РАВ4 2001 года
Ширина колеи может оказывать существенное влияние на ощущения от вождения авто, поэтому: чем больше расстояние между колесами на одной и той же оси – тем лучше автомобиль входит в крутые повороты на трассе.
Радиус разворота автомобиля Тойота РАВ4 2001 года
Радиус разворота дает представление о наименьшем радиусе воображаемого круга, по которому автомобиль может выполнить разворот на дороге. Данная габаритная величина – хороший индикатор, который говорит о маневренности авто.
Клиренс автомобиля Тойота РАВ4 2001 года
Дорожный просвет или же по ненашенскому – клиренс – измеряет расстояние между плоской поверхностью и самой нижней точкой днища. Клиренс должен замеряться на стандартных размерах шин.
Коэффициент аэродинамического сопротивления автомобиля Тойота РАВ4 2001 года
Коэффициент сопротивления описывает аэродинамические характеристики автомобиля, указывая на уровень сопротивления воздуха при движении. Дизайн автомобиля очень сильно влияет на этот показатель, поэтому для седанов коэффициент сопротивления будет меньшим, нежели у кроссоверов и джипов из-за их угловатых очертаний.
2001 Тойота РАВ4 размеры интерьера
| Head Room — Front | 104.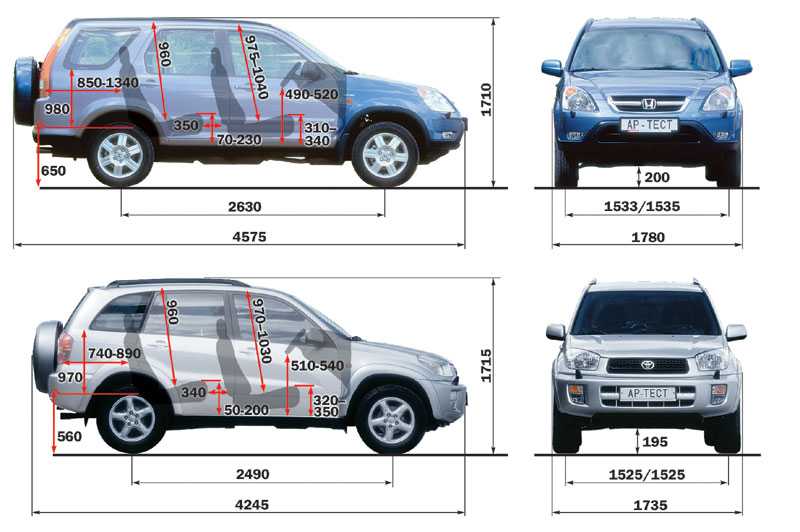 902 см 902 см
|
| Head Room — Rear | 97.536 см |
| Hip Room — Front | 135.636 см |
| Hip Room — Rear | 118.11 см |
| Leg Room — Front | 107.696 см |
| Leg Room — Rear | 82.804 см |
| Shoulder Room — Front | 137.414 см |
| Shoulder Room — Rear | 136.398 см |
Габариты салона автомобиля Тойота РАВ4 2001
Высокие водители должны с особым пристрастием проверять габариты салона 2001 Тойота РАВ4, дабы быть уверенными в том, что ничто не помешает получить удовольствие от вождения.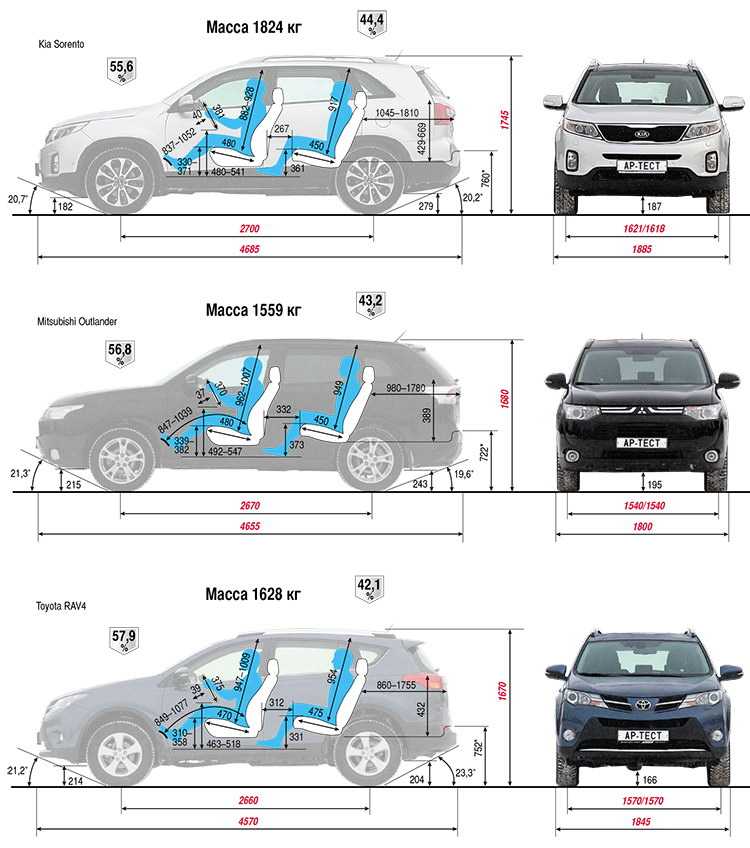
Размеры конкурентов
-
Размеры Шевроле Трекер 2001
-
Размеры Крайслер ПТ Крузер 2001
-
Размеры Форд Куга 2001
-
Размеры Сузуки Гранд Витара 2001
-
Размеры Сузуки Витара 2001
-
Размеры Сузуки Гранд Витара ХЛ-7 2001
Размеры модели Тойота РАВ4 по годам
- 2015
- 2014
- 2013
- 2012
- 2011
- 2010
- 2009
- 2008
- 2007
- 2006
- 2005
- 2004
- 2003
- 2002
- 2001
- 2000
- 1999
Другие модели Тойота 2001 года
Длина, ширина, высота, глубина – Элементарная математика
Длина, ширина, высота, глубина
Вне уроков математики контекст обычно определяет наш выбор словаря: длина строки, ширина строки дверной проем, высота флагштока, глубина бассейна.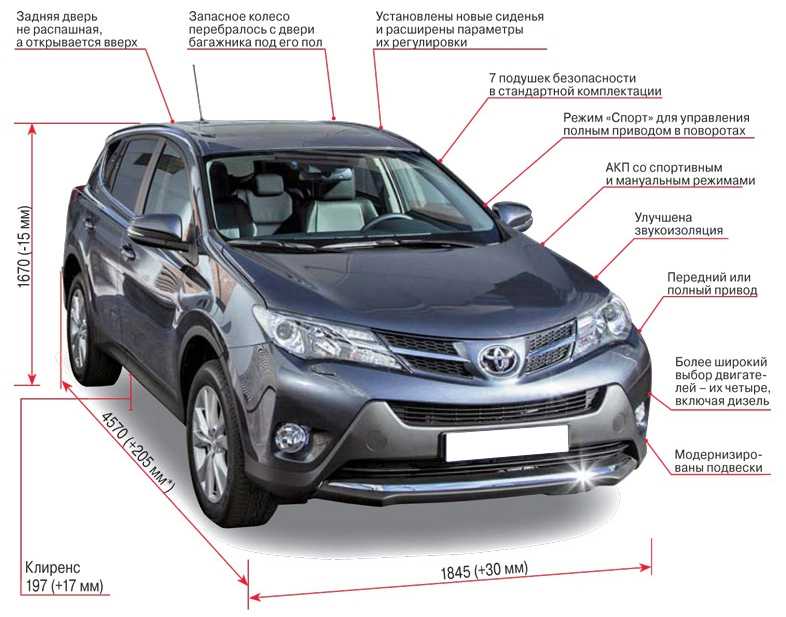 Но при описании прямоугольников или объектов в форме кирпича выбор лексики кажется менее ясным.
Но при описании прямоугольников или объектов в форме кирпича выбор лексики кажется менее ясным.
Вопрос: Должны ли мы обозначать два измерения прямоугольника длина и ширина ; или ширина и высота ; или даже длина и высота ? Существует ли «правильное» использование терминов длина , ширина , высота и глубина ?
Прямоугольники различной формы и положения.
Выбор лексики здесь полностью зависит от ясности и отсутствия двусмысленности. Математика не предписывает правил «правильного» использования этих терминов в данном контексте. В математике, как и везде, специализированная лексика служит для ясного и недвусмысленного общения. В этом случае наша естественная манера говорить дает нам некоторые ориентиры.
Длина: Если вы решите использовать слово длина , оно должно относиться к самому длинному измерению прямоугольника. Подумайте, как бы вы описали расстояние вдоль дороги: это длинное расстояние, длина дороги. (Слова вдоль , длина и длина th связаны друг с другом.) Расстояние поперек дороги говорит о том, насколько шириной дорога проходит от одной стороны до другой. это ширина дороги. (Слова wid e и wid th тоже родственны.)
Подумайте, как бы вы описали расстояние вдоль дороги: это длинное расстояние, длина дороги. (Слова вдоль , длина и длина th связаны друг с другом.) Расстояние поперек дороги говорит о том, насколько шириной дорога проходит от одной стороны до другой. это ширина дороги. (Слова wid e и wid th тоже родственны.)
Когда прямоугольник нарисован «наклонно» на странице, как здесь, обычно яснее всего обозначить длинную сторону как «длину», а другую боковая «ширина», как если бы вы маркировали дорогу.
Наклонный прямоугольник.
Высота: Когда прямоугольник нарисован с горизонтальной и вертикальной сторонами, слово высота дает понять, какой размер имеется в виду; высота обозначает, как высота (высота) прямоугольника. Это упрощает указание другого измерения — ширины прямоугольника от стороны до стороны — с помощью слова ширина . И если поперечный размер больше, чем высота, также допустимо называть его длиной прямоугольника, так как это не создает путаницы.
И если поперечный размер больше, чем высота, также допустимо называть его длиной прямоугольника, так как это не создает путаницы.
Прямоугольники различной ориентации.
Обратите внимание, что в этом случае, когда используется высота , сравнительный размер не имеет значения. Потому что высота всегда вертикальна, размеры, ширина или высота могут быть больше.
Когда слово высота используется в сочетании с основанием , оно имеет особое значение, которое не обязательно относится к вертикальному измерению.
Для некоторых непрямоугольных форм термины длина , высота или ширина остаются неясными, четко показывают, что вы имеете в виду, и ссылаются на них как на «это расстояние» или «это измерение».
Трехмерность
При названии размеров трехмерной фигуры единственное правило: иметь смысл и быть ясным . Это поможет использовать ярлыки.
Когда фигура «ровная», высота явно относится к вертикальному измерению — насколько высока фигура — независимо от того, является ли это измерение наибольшим, наименьшим или чем-то средним; длина (если вы используете это слово) относится к большему из двух других измерений. Но вы также можете ссылаться на другие измерения как на 9.0005 ширина и глубина (и они в значительной степени взаимозаменяемы, в зависимости от того, что «кажется» широким или глубоким в фигуре). См. эти примеры.
Но вы также можете ссылаться на другие измерения как на 9.0005 ширина и глубина (и они в значительной степени взаимозаменяемы, в зависимости от того, что «кажется» широким или глубоким в фигуре). См. эти примеры.
Когда высота неясна — например, если фигура не «ровная» — люди не могут знать, что имеется в виду под шириной, глубиной или высотой без меток, хотя длина обычно по-прежнему считается относящейся к самому длинному измерению на фигура. И, как и в случае с двумя измерениями, такие термины, как «длина», «ширина» и «высота», не будут казаться естественными или понятными для некоторых форм, таких как теннисный мяч.
Что в слове?
Длина , Ширина , Высота и Глубина — существительные, получены из прилагательных Long
 (Одинокий т в высота является современным. Устаревшие формы включают высотах и highth , и люди до сих пор часто произносят это слово.)
(Одинокий т в высота является современным. Устаревшие формы включают высотах и highth , и люди до сих пор часто произносят это слово.) Другие пары прилагательное-существительное в английском языке также связаны таким же образом: например, hale как «здоровый и сердечный» и health (но hale , за исключением этого выражения, теперь в основном заменяется на «здоровый»).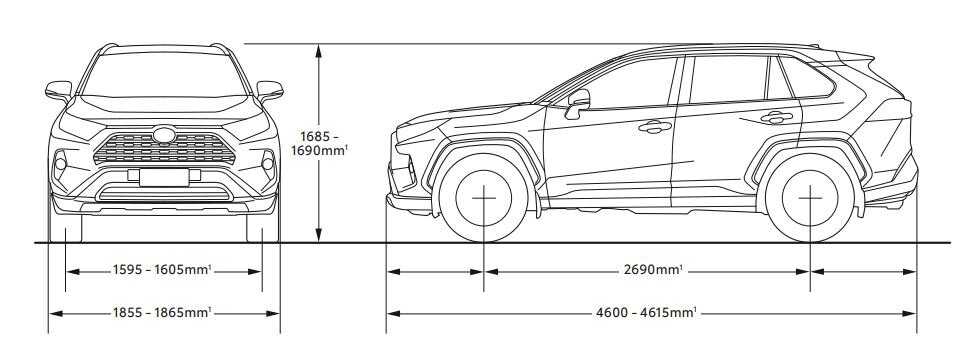
1.4 Анализ размеров | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Находить размерности математического выражения, включающего физические величины.
- Определите, является ли уравнение, включающее физические величины, размерно-согласованным.
Размерность любой физической величины выражает ее зависимость от основных величин как произведение символов (или степеней символов), представляющих основные величины. (Рисунок) перечислены основные величины и символы, используемые для их измерения. Например, говорят, что измерение длины имеет размерность L или L  Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L 3 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L 3 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
| Базовое количество | Обозначение размера |
|---|---|
| Длина | л |
| Масса | М |
| Время | Т |
| Текущий | я |
| Термодинамическая температура | Θ |
| Количество вещества | Н |
| Сила света | Дж |
Физики часто используют квадратные скобки вокруг символа физической величины, чтобы представить размеры этой величины. Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Важность концепции размерности проистекает из того факта, что любое математическое уравнение, связывающее физические величины, должно быть размерно-согласованным, что означает, что уравнение должно подчиняться следующим правилам:
- Каждый член выражения должен иметь одинаковые размеры; нет смысла прибавлять или вычитать количества разной размерности (вспомните старую поговорку: «Нельзя складывать яблоки и апельсины»). В частности, выражения по обе стороны равенства в уравнении должны иметь одинаковые размерности.
- Аргументы любых стандартных математических функций, таких как тригонометрические функции (такие как синус и косинус), логарифмы или экспоненциальные функции, которые появляются в уравнении, должны быть безразмерными.
 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Если какое-либо из этих правил нарушается, уравнение не является размерно-согласованным и не может быть правильной формулировкой физического закона. Этот простой факт можно использовать для проверки опечаток или алгебраических ошибок, чтобы помочь вспомнить различные законы физики и даже предложить форму, которую могут принять новые законы физики. Это последнее использование измерений выходит за рамки этого текста, но вы, несомненно, узнаете об этом позже в своей академической карьере. 9{2} [/латекс] и [латекс] 2\pi r. [/latex] Одно выражение — это длина окружности круга радиусом r , а другое — его площадь. Но что есть что?
Стратегия
Естественная стратегия — искать информацию, но это может занять время, чтобы найти информацию из авторитетного источника. Кроме того, даже если мы считаем источник авторитетным, мы не должны доверять всему, что читаем. Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
[латекс] [2\pi r]=[2]·[\pi ]·[r]=1·1·\text {L}=\text{L,} [/latex]
, так как константы [latex] 2 [/latex] и [latex] \pi [/latex] безразмерны, а радиус [latex] r [/latex ] — это длина. Мы видим, что [латекс] 2\pi r [/латекс] имеет размерность длины, что означает, что он никак не может быть площадью.
Мы исключаем [латекс] 2\pi r [/латекс], потому что его размеры не соответствуют площади. Мы видим, что [латекс] \pi {r}^{2} [/латекс] согласуется по размерам с областью, поэтому, если нам нужно выбирать между этими двумя выражениями, [латекс] \пи {г}^{2} [/latex] — это то, что нужно выбрать. {2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
{2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
Стратегия
По определению размерной согласованности нам нужно проверить, что каждый член данного уравнения имеет те же размерности, что и другие члены этого уравнения, и что аргументы любых стандартных математических функций безразмерны.
Решение
- В этом уравнении нет ни тригонометрических, ни логарифмических, ни экспоненциальных функций, поэтому нам достаточно посмотреть на размеры каждого члена, входящего в уравнение. Есть три термина, один в левом выражении и два в выражении справа, поэтому мы рассмотрим каждый по очереди: 9{2}}{s})]=1.\hfill \end{массив} [/latex]
Два члена имеют разные размерности — это означает, что уравнение не является размерно-согласованным. Это уравнение — еще один пример «бессмыслицы».
Значение
Если мы доверяем людям, эти виды размерных проверок могут показаться ненужными. Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Проверьте свое понимание
Соответствует ли размерность уравнения v = at ?
Показать решение
Еще один момент, о котором следует упомянуть, — это влияние операций исчисления на размерности. Мы видели, что размеры подчиняются правилам алгебры, как и единицы, но что происходит, когда мы берем производную одной физической величины по отношению к другой или интегрируем физическую величину по другой? Производная функции — это просто наклон линии, касательной к ее графику, а наклоны — это отношения, поэтому для физических величин v и t , мы имеем, что размерность производной v по отношению к t есть просто отношение размерности v к размерности t :
[латекс] [ \frac{dv}{dt}]=\frac{[v]}{[t]}. [/latex]
[/latex]
Точно так же, поскольку интегралы представляют собой просто суммы произведений, размерность интеграла v относительно t — это просто размерность v , умноженная на размерность t :
[латекс] [\int vdt]=[v]·[t]. [/latex]
По тем же соображениям аналогичные правила справедливы для единиц физических величин, полученных из других величин путем интегрирования или дифференцирования.
Резюме
- Размерность физической величины — это просто выражение основных величин, из которых она получена.
- Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов. 9{2}; [/latex] (c) [latex] v=s\text{/}t; [/latex] (d) [latex] a=v\text{/}t. [/latex]
Показать решение
Рассмотрим физические величины [латекс] m, [/латекс] [латекс] s, [/латекс] [латекс] v, [/латекс] [латекс] а, [/латекс] и [латекс] t [/латекс ] с размерами [ м ] = M, [ s ] = L, [ v ] = LT –1 , [ a ] = LT –2 , и [
6 t 90] = T.
 Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсек. дуги ; (e) L = mvr .
Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсек. дуги ; (e) L = mvr .Предположим, что количество [латекс] s [/латекс] — это длина, а количество [латекс] t [/латекс] — это время. Предположим, что величины [латекс] v [/латекс] и [латекс] а [/латекс] определены как v = ds / dt и a = dv / dt . а) Какова размерность числа 9?{–3}, [/latex] и [t] = T. (a) Какова размерность [latex] \int \rho dV? [/latex] (b) Каков размер dV / dt ? в) Каков размер [латекс] \rho (dV\text{/}dt)? [/latex]
Формула длины дуги говорит, что длина [латекс] s [/латекс] дуги, опирающейся на угол [латекс] Ɵ [/латекс] в окружности радиусом [латекс] r [/латекс], определяется выражением уравнение [латекс] s=rƟ.



 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.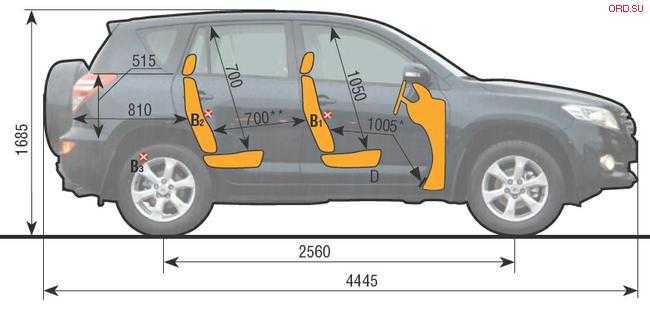 Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсек. дуги ; (e) L = mvr .
Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсек. дуги ; (e) L = mvr .